
I rompicapi geometri da sempre stimolano l’ingegno e aguzzano la mente, oltre la curiosità degli appassionati, offrendo sfide che mettono alla prova le capacità cognitive e di ragionamento di vario tipo. Uno di questi enigmi, solo apparentemente semplice e di facile risoluzione, ha in realtà messo alla prova la mente di esperti e studiosi.
Il problema dei nove punti
Uno dei rompicapi geometrici più famosi è il cosiddetto problema dei nove punti, un enigma che prevede la disposizione di nove punti su un piano, organizzati in una griglia 3 x 3. La sfida, e la soluzione, consiste nel collegare tutti i nove punti utilizzando solo quattro segmenti di linea retta, però, senza mai sollevare la penna dal foglio e senza ripassare su un segmento.

A prima vista questo problema sembra semplice e di facile soluzione ma molte persone trovano invece difficile venirne a capo con una soluzione corretta che rispetti le indicazioni date. La soluzione richiede un pensiero fuori dall’ordinario. Molti tentano di collegare i punti rimando entro la superficie segnata dalla griglia.
Invece, la soluzione corretta richiede di estendere le linee oltre la griglia 3 x 3, che rappresenta solo un confine immaginario. Le istruzioni non dicono che non si deve tracciare i segmenti necessariamente entro l’area della griglia, questo è un limite che il nostro stesso cervello si impone. Utilizzando il pensiero laterale, invece, la soluzione arriva facilmente.
Il paradosso dell’area scomparsa
Un altro celebre rompicapo geometrico è il paradosso dell’area scomparsa. Questo enigma presenta due figure apparentemente identiche e formate dalle stesse tessere geometriche. Ma una differenza c’è ed è paradossale: una delle due figure sembra avere un’area in meno rispetto all’altra. Come è possibile? Ecco la spiegazione al paradosso dell’area scomparsa.
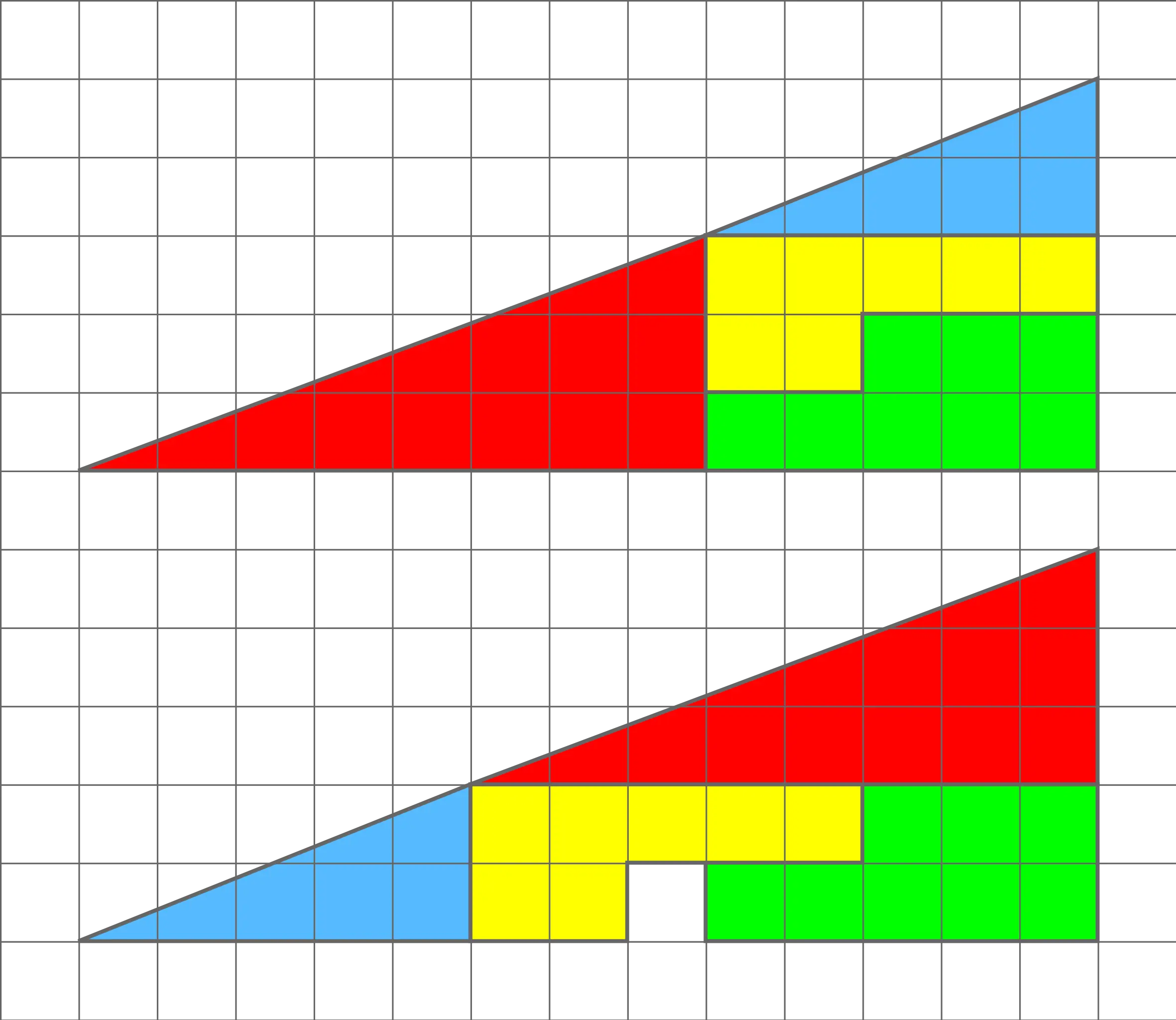
La spiegazione di questo apparente paradosso è legata al fatto che le due figure, in realtà, non sono perfettamente identiche. Sebbene le tessere geometriche siano le stesse, esse differiscono per disposizione e ciò crea una piccola differenza negli angoli in modo che una figura sia leggermente più grande rispetto all’altra.
Questa differenza è difficile da cogliere a prima vista e il paradosso dell’area scomparsa è un buon esempio per dimostrare come la percezione visiva possa essere ingannata. Per non cadere in questo errore è necessario affidarsi all’analisi attenta e critica della geometria, delle piccole variazioni delle dimensioni e degli angoli che possono fare la differenza.
La torre di Hanoi
Un altro famoso rompicapo di tipo geometrico è quello della torre di Hanoi. Questo rompicapo, conosciuto anche come Torre di Lucas dal nome dell’inventore, consiste in una serie di dischi di dimensioni differenti impilati in ordine decrescente su un paletto con l’obiettivo di spostarli su una latro paletto mantenendone l’ordine.

Il terzo paletto funge da aiuto e vige la regola che un disco più grande non può essere posizionato sopra uno più piccolo. La soluzione è di tipo matematico e si basa su un numero minimo di mosse necessario per risolvere e completare l’enigma. La formula è 2n -1 dove “n” sta per il numero dei dischi. Ad esempio, per spostare 3 dischi sono necessarie almeno 7 mosse.
La torre di Hanoi rappresenta un rompicapo che ha appassionato migliaia di persone dall’epoca della sua invenzione che risale al 1883 a opera del matematico Eduard Lucas e a cui è legata la leggenda secondo cui in un tempio indù non ben specificato esiste un gruppo di monaci che da allora è impegnato nella risoluzione del problema.
Il valore dei rompicapi geometrici
Gli enigmi geometrici possono rappresentare uno strumento didattico utile per favorire lo sviluppo dei pensiero critico e la capacità di ragionamento logico. La loro formulazione, infatti, richiede l’analisi della situazione, la formulazione di ipotesi e di concepire soluzioni in base a un processo che implica riflessione e pensiero critico.

Questo è un processo che stimola l’apprendimento attivo e la comprensione di concetti matematici e geometrici in modo intuitivo con beneficio di molti processi cognitivi. La mente è costretta a lavorare in condizioni di incertezza, stimolando l’autonomia cognitiva, la gestione dell’errore la riformulazione di strategie mirate alla soluzione, cosa non scontata.
Tutto ciò promuove una maggiore flessibilità mentale, che non è utile solo nell’ambito scolastico o lavorativo, ma nella vita generale di tutti i giorni, dove è fondamentale sapere prendere soluzioni e decisioni rapide ed efficaci valutando diversi scenari alternativi e soluzioni innovative, in base alla riformulazione di strategie e alla gestione degli errori.








